Алгоритмы Сортировки. Часть 1
Все из существующих ныне способов сортировки отличаются друг от друга по скорости выполнения, понятности и длине кода, по красоте решения. Зачастую в код уже разработанного алгоритма вносятся какие-либо изменения и так возникает множество решений, некоторые и с которых мы и попробуем сейчас рассмотреть.
Однако, следует отметить что изучение алгоритмов совсем не лёгкая задача, здесь требуется внимательное рассмотрение каждой строчки. Конечно если Вы воспользуетесь кнопками Ctrl+C и Ctrl+V Ваша программа не станет хуже работать, но на мой взгляд, нет ничего хуже когда программист сам до конца не понимает, как работает его программа.
Итак, начнём.
Сортировка выбором
И начнём мы с сортировки выбором. Хотя этот алгоритм и не является самым быстрым, но я решил начать с него потому что, на мой взгляд он наиболее прост для понимания. Суть алгоритма состоит в том, что бы в исходном массиве найти наименьший элемент, а затем поменять местами первый элемент в списке с найденным. После того, находиться наименьший их оставшихся и меняется со вторым элементом. И так до тех пор пока весь список не будет отсортирован.
Таким образом понадобиться N+(N-1)+(N-2)+...+1 или N*N проходов чтобы отсортировать список.
| Листинг 1. Сортировка выбором
|
procedure SellectionSort( var a: array of integer; min,
max: Integer);
var
i, j, best_value, best_j: longint;
begin
for i:=min to max do begin
best_value:=a[i];
best_j:=i;
for j:=i+1 to max do begin
if a[j]<best_value then begin
best_value:=a[j];
best_j:=j;
end;
end;
a[best_j]:=a[i];
a[i]:=best_value;
end;
end;
|
Переменными min и mах можно ограничить область списка в которой, будет выполнена сортировка. Что бы отсортировать весь массив необходимо записать следующее
| Листинг 2. Код Delphi/Pascal
|
| SellectionSort(a, 0, high(a));
|
Сортировка вставкой
Это тоже предельно простой для понимания алгоритм. Идея в том что бы создать новый массив, а затем последовательно вставлять в новый массив элементы из старого массива, чтобы созданный массив был всё время упорядоченным.
| Листинг 3. Сортировка вставкой
|
procedure InsertionSort( var a: array of integer; N: integer);
var
B: array [0..10000] of integer;
i, j: integer;
begin
for i:=0 to N do begin
j:=i;
while (j>1) and (B[j-1]>A[i]) do begin
B[j]:=B[j-1];
j:=j-1;
end;
B[j]:=A[i];
end;
for i:=0 to N do
A[i]:=b[i];
end; |
Если внимательно посмотреть на реализацию алгоритма, то сразу же заметим что для его выполнения необходимо больше,, чем N*N проходов, поэтому в приложениях, где скорость выполнения кода критична, подобный алгоритм использовать не актуально.
Пузырьковая сортировка
Чаще всего используется для сортировки частично упорядоченных списков, так как именно для них скорость выполнения максимальна и может равняться O(N), где N количество элементов массива, а O время одного прохода через цикл. Этот алгоритм в исходном списке ищет пары цифр, которые следуют не по порядку и затем меняет их местами.Процесс повторяется до тех пор пока весь список не будет отсортированным. На рисунке изображен пример сортировки данным методом.
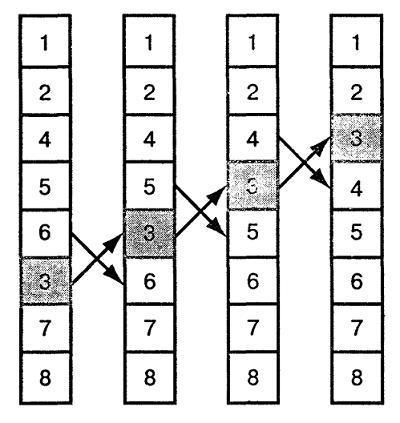
На рисунке можно проследить за перемещение элемента, который изначально был ниже чем после сортировки. Во время прохода цикла, элемент изменяет свою позицию на одну позицию ближе к своему конечному месту. На рисунке элемент двигается к вершине, как пузырёк воздуха к поверхности воды. Этот эффект и дал название алгоритму пузырьковой сортировке.
| Листинг 4. Пузырьковая сортировка
|
procedure BubbleSort( var a: array of integer; min, max: Integer);
var
i, j, tmp: integer;
begin
for i:=min to max do
for j:=min to max-i do
if A[j]>A[j+1] then
begin {Обмен элементов}
tmp:=A[j];
A[j]:=A[j+1];
A[j+1]:=tmp;
end;
end; |
Быстрая сортировка.
При этом виде сортировке массив разбивается на две части, а затем рекурсивно вызывает сама себя для их сортировки. Притом элементы первой части меньше любого элемента второй части.
Рассмотрим данный вид сортировке на примере:
Если алгоритм вызывается для списка, который содержит нуль или один элемент, то подписок уже отсортирован и процедура заканчивается, в противном случае выбирается один элемент, относительно которого список разбивается на две части, в первый подписок идут элементы меньше выбранного, во второй больше. И затем, как уже было сказано, она рекурсивно вызывает сама себя для сортировки обои подсписков.
| Листинг 5. Быстрая сортировка
|
procedure QuickSort( var a: array of integer; min, max: Integer);
Var
i,j,mid, tmp : integer;
Begin
if min<max then begin
mid:=A[min];
i:=min-1;
j:=max+1;
while i<j do begin
repeat
i:=i+1;
until A[i]>=mid;
repeat
j:=j-1;
until A[j]<=mid;
if i<j then begin
tmp:=A[i];
A[i]:=A[j];
A[j]:=tmp;
end;
end;
QuickSort(a, min,j);
QuickSort(a, j+1,max);
end;
end;
|
Стоит также заметить, что такой сортировкой лучше всего пользоваться для упорядочевания массивов элементы в которых следуют абсолютно, случайно. В то время как, если список практически упорядочен, разумнее будет использовать пузырьковую сортировку. К тому же если список достаточно длинный, то алгоритм вызовет глубокую рекурсию и возможно переполнение стёка и как следствие зависание или аварийный выход программы.
Сортировка методом Шелла.
Ещё один метод сортировки - это сортировка методом Шелла.Основная идея этого алгоритма заключается в том, чтобы в начале ycтpанить массовый беспорядок в массиве, сравнивая далеко стоящие друг от друга элементы. Как видно, интервал между сравниваемыми элементами постепенно уменьшается до единицы. Это означает, что на поздних стадиях сортировка сводится просто к перестановкам соседних элементов (если, конечно, такие перестановки являются необходимыми).
| Листинг 6. Сортировка методом Шелла
|
procedure TForm1.SortShell( var a: array of real; N: Integer);
var
h:Variant;
c:Boolean;
g:Integer;
i:Integer;
j:Integer;
tmp:Real;
begin
h:=1;
g:=0;
repeat
h:=3*h+1
until (h>=n);
if (h>n) then begin
h:= h/3;
g:=h;
end;
n:=n-1;
repeat
i:=g;
repeat
j:=i-g;
c:=True;
repeat
if a[j]<=a[j+g] then begin
c:=False;
end
else begin
Tmp:=a[j];
a[j]:=a[j+g];
a[j+g]:=Tmp;
end;
j:=j-1
until not((j>=0)and(C));
i:=i+1
until not(i<=n);
h:=g;
h:=h/3;
g:=h;
until not(g>0);
end; |
Заключение.
В данной статье была предпринята попытка объяснить наиболее часто применяемые алгоритмы сортировки. Однако рассказать о всех аспектах реализации различных алгоритмов в одной статье довольно сложно, и статья получается перенасыщенная информацией, поэтому я решил разбить её на две части и сейчас вторая уже готовиться к выходу. В ней планируется рассказать о более специфических алгоритмах, сортировке не только цифр, но и слов, как русского так и английского языка, а также об обратном процессе сортировки - перемешивания.
Удачи!
P.S. Замечания, пожелания и дополнения к этой статье просим оставлять на форуме.
Автор: Спиридонов Виталий
Источник: www.noil.pri.ee
|

