Программирование -> Delphi / Pascal -> Алгоритмы Сортировки. Часть 2

Это вторая часть статьи, посвященная алгоритмам сортировки. Если вы пропустили первую, то её можно найти на моём сайте, перейдя по этой ссылке . В этой же части я продолжу объяснения о существует ныне методах сортировки, а также попробую рассказать о других примерах, которые хотя и не являются алгоритмами сортировки, но тесно связаны с этой темой, и возможно, они вам пригодиться когда вы столкнётесь с решением реальной задачи.

Сортировка слиянием

Сортировка слиянием - этот рекурсивный алгоритм. Он, также как и быстрая сортировка(описано в первой части), делит список на две части, и затем рекурсивно вызывает сам себя для их дальнейшего упорядочивания. Она делит список на две равные части, после чего подсписки рекурсивно сортируются и сливаются для того что бы образовать полностью отсортированный список.

Процесс объединения, наверно, наиболее интересная часть алгоритма и её понять, довольно, не сложно. Подсписки объединяются в рабочий массив, а результат копируется в исходный список. Однако, следует учитывать что при сортировки слишком большого массива могут возникнуть проблемы с составлением рабочего массива. Из-за большого числа сортируемых элементов, программа может обращаться к файлу подкачки что снижает её скорость, также пагубно влияет на время копирования данных из одного массива в другой. Но время выполнения можно увеличить, если применять в связку сортировкой слиянием с другой сортировкой, например с сортировкой вставками. Для этого необходимо выбрать некоторое число элементов массива при достижении которого рекурсия будет остановлена и массив будет досортирован другим методом. Это можно сделать примерно так:

Листинг 1. Код Delphi/Pascal

if (max-min)<StopIndex then begin SelctionSort(a, min, max); exit; end;

StopIndex - это и есть то число которое Вы выбрали для остановки рекурсии.Сам алгоритм в чистом виде выглядит так:

Листинг 2. Сортировка слиянием

procedure MergeSort( var ar1, ar2: array of Integer; min, max: Integer); var middle, int1, int2, int3: Integer; begin if min<max then begin //в противном случае массив состоит //из 1-го элемента и упорядочен. middle:=min div 2+max div 2; // рекурсивно сортируем подсписки MergeSort(ar1, ar2, min, middle); MergeSort(ar1, ar2, middle+1, max); int1:=min; //указатель на 1-й массив int2:=middle+1; //указатель на 2-й массив int3:=min; //указатель на объединённый массив //объединение сортированных массивов while (int1<=middle) and (int2<=max) do begin if ar1[int1] then begin ar2[int3]:=ar1[int1]; int1:=int1+1; end else begin ar2[int3]:=ar1[int2]; int2:=int2+1; end; inc(int3); end; // очистка не пустого списка while (int1<=middle) do begin ar2[int3]:=ar1[int1]; int1:=int1+1; int3:=int3+1; end; while (int2<=middle) do begin ar2[int3]:=ar1[int2]; int2:=int2+1; int3:=int3+1; end; end; //приравнивание входящих массивов for int1:=min to max do ar1[int1]:=ar2[int1]; end;

Этот алгоритм работает обычно медленней, чем быстрая сортировка, однако у него есть ряд преимуществ: во первых он показывает стабильные результаты при сортировке определённого количества данных, в то время как при быстрой сортировке эти результаты могут довольно сильно различаться(см табл). Во-вторых, при большом количестве повторяющихся элементов программа не уходит в глубокую рекурсию.

Результата сравнения сортировки слиянием быстрой сортировкой приведены в таблице. Для тестов использовался компьютер с процессором Pentium-133, 16-Ram. Количество сортируемых элементов равнялось 1млн.

Диапазон значений	Время сортировки слиянием (сек)	Время быстрой сортировки(сек)
1-10млн	4.72	2,75
1-1000	4.67	16.12
1-100	4.75	194.18

Сортировка подсчётом

Сортировка подсчётом - специализированный алгоритм, который работает невероятно быстро, если элементами массива являются целые числа, со значениями, которые занимают, относительно узкий диапазон(диапазон значений должен быть сравним с длинной массива). Пока выполняются эти условия алгоритм работает отлично. Для примера можно привести результат сортировки 1-го миллиона элементов со значением от 1-10000, на том же компьютере с процессором Pentium-133. Время быстрой сортировки было равно 3,93 секунды, результат же сортировки подсчётом был 0,37секунды, то есть быстрее в 10 раз.

Большая скорость выполнения достигает за счёт того, что в алгоритме не используются операции сравнения. Без них алгоритм сортировки может упорядочивать значения за время равное O(N).

Исходный текст алгоритма подсчётом, довольно, короткий и кажется простым, в действительности он очень тонок.

Листинг 3. Сортировка подсчётом

procedure CountiongSort( var ar: array of integer; min, max: integer); var counter: array [0..100000] of integer; i, j, index: Integer; begin // заполняем массив нулями for i:=0 to high(counter) do tmpA[i]:=0; for i:=min to max do begin counter[ar[i]]:=counter[ar[i]]+1; end; // устанавливаем значение в правильную позицию index:=min; for i:=min to high(counter)-1 do begin for j:=0 to counter[i]-1 do begin ar[index]:=i; index:=index+1; end; end; end;

Давайте попробуем его рассмотреть. Вначале создаётся массив для подсчёта элементов имеющих определённое значение, и устанавливает все значения равными нулю. Затем алгоритм вычисляет сколько раз в списке встречается каждый элемент и увеличивает значение соответствующей записи счётчика на 1. Или иными словами, при исследовании элемента массива под номером i программа увеличивает значение counter[ar[i]].И конце, алгоритм проходит через весь массив счётчиков, помещая определённое число элементов в отсортированный массив. Для каждого значения i от 1 до N он добавляет counter[i] элементов со значением i.

Сортировка шейкером

Сортировка шейкером, чаще всего, применяется для упорядочивания очень больших массивов, которые возможно находятся на жёстком диске. Этот алгоритм за один проход цикла выбирает наибольший и наименьший алгоритм и помещает их соответственно в начало и конец списка. Затем операция повторяется и сортируются остальные элементы. Таким образом для сортировки всего массива понадобиться N\2 проходов цикла.
Код алгоритма должен выглядеть примерно так:

Листинг 4. Сортировка подсчётом

procedure ShakerSort( var ar: array of integer; min, max: Integer); var n, i, j, tmp: Integer; begin n:=max; for i:=1 to (n div 2) do begin if ar[i]>ar[i+1] then begin min:=i+1; max:=i; end else begin min:=i; max:=i+1; end; for j:=i+2 to (n-i+1) do if ar[j]>ar[Max] then max:=j else if ar[j]<ar[Min] then min:=j; // end; else if // end; for {Обмен элементов} tmp:=ar[i]; ar[i]:=ar[min]; ar[min]:=tmp; if max=i then max:=min; // end; if tmp:=ar[n-i+1]; ar[n-i+1]:=ar[max]; ar[max]:=tmp; end; end;

Краткие Выводы

Перед тем как перейти ко второй части статьи хочу сделать общий вывод изученного материала. Мы с вами рассмотрели восемь различных способов сортировки данных и я думаю, что это достаточный багаж знаний. Возможно, кто-то спросит, а зачем писать сложные алгоритмы, если есть сортировка вставками, которая реализуется всего в пару строк и в её работе всё понятно. Да, в чём то он будет прав, для сортировки не больших массивов алгоритм сортировки вставками подходит не плохо, но если массив будет состоять из миллиона элементов и вы запустите его сортироваться методом вставок, то компьютер надолго задумается. Поэтому всегда надо отдавать себе отчёт в том какая из сортировок наиболее желательна в конкретном случае. И для того что бы Вам было легче решить какой именно метод использовать, я хочу привести такую таблицу.

Алгоритм	Преимущества	Недостатки
Сортировка Выбором	Очень прост, Быстро сортирует небольшие списки	Медленно работает с большими списками
Сортировка вставками	Очень прост, Быстро сортирует небольшие списки	Очень медленно работает с большими списками
Пузырьковая сортировка	Быстро работает для почти отсортированных списков	Медленно работает в остальных случаях
Быстрая сортировка	Быстро сортирует большие списки	Работает некорректно при большом количестве одинаковых значений
Метод Шелла	Сортирует дробные числа	Требует пространства памяти для хранения временных значений
Сортировка слиянием	Быстро сортирует большие списки	Работает медленнее, чем быстрая сортировка
Сортировка подсчётом	Очень быстро работает, если разброс входных значений не велик	Медленно работает в случае если разброс составляет >log(N)
Сортировка Шейкером	Сортирует данные на жёстком диске	Работает медленнее, чем быстрая сортировка

На этом мы закончим рассмотрение самих алгоритмов сортировки и перейдём к другим примерам связанным с этой темой.

Перемешивание

Сейчас рассмотрим обратный сортировке процесс, а именно перемешивание. Это значит что из упорядоченного состояния мы будем переводить данные в неупорядоченные. Сам алгоритм довольно прост, но всё же кратко расскажу о принципе его действия.

Для каждой позиции списка алгоритм случайным образом выбирает элемент. При этом рассматриваются элементы из ещё не помещённых на своё место. Затем выбранный элемент меняется местами со стоящим в этой позиции элементом. При этом не имеет значения был ли список отсортирован самого начала или нет. Программы всё равно перемешает элементы списка.

Сам код выглядит так:

Листинг 5. Перемешивание

procedure RandomizeArray( var ar: array of integer; min, max: Integer); var i, range, pos, tmp: Integer; begin range:=max-min+1; Randomize; for i:=min to max-1 do begin pos:=min+random(range); tmp:=ar[pos]; ar[pos]:=ar[i]; ar[i]:=tmp; end; end;

Сортировка строк

Если вы внимательно посмотрите на код представленных сортировок, то заметите, что для некоторых из них не имеет значение какие данные сортировать. Итак в такими сортировками являются: сортировка вставками, выбором, пузырьковая сортировка, быстрая сортировка, сортировка слиянием и сортировка шейкером. Возьмём для примера быструю сортировку и переделаем ей для упорядочивания строк, при это никакого значения играть не будет какую раскладку вы используете.
То что получилось у меня вы можете увидеть ниже.

Листинг 6. Сортировка строк

procedure QuickSort( var a: array of string ; min, max: Integer); Var i,j: integer; mid, tmp: string ; Begin if min<max then begin {массив из одного элемента тривиально упорядочен} mid:=A[min]; i:=min-1; j:=max+1; while i<j do begin repeat i:=i+1; until A[i]>=mid; repeat j:=j-1; until A[j]<=mid; if i<j then begin tmp:=A[i]; A[i]:=A[j]; A[j]:=tmp; end; end; QuickSort(a, min,j); QuickSort(a, j+1,max); end; end;

Поиск в отсортированном массиве

Когда необходимо найти произвольный элемент в массиве самое первое что приходит на ум это перебрать все значения массива и сравнить их с искомым. Однако применять этот метод для поиска в отсортированном массиве значит не рационально использовать ресурсы компьютера. Для отсортированных массивов лучше применять двоичный поиск. Его идея заключается в следующем сравнить искомый элемент с элементом в серединой массива, если искомый элемент меньше элемента в середине массива, то подобным же образом исследовать первую половину массива, если больше - то вторую, если равен - то возвращается его индекс. Лучше всего понять всё вышесказанное, взглянув на рисунок. На нём показан процесс нахождения числа 44.

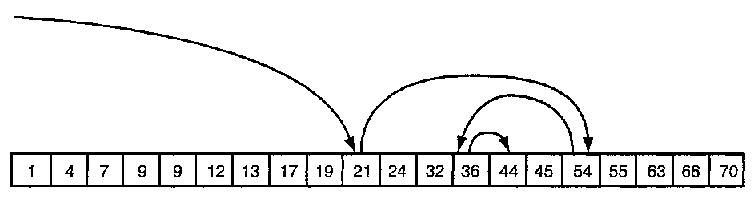
Сам код алгоритма двоичного поиска выглядит так:

Заключение

На этом думаю поставить точку. Как всегда, свои замечание по прочитанной статьи вы можете оставить на форуме . Если что-то не получилось скачать исходник можно здесь

Автор: Спиридонов Виталий
Источник: www.noil.pri.ee